CHAPTER 12 OVERVIEW OF SEPARATE INVESTIGATIONS

After the ESTONIA had changed course at the waypoint she sailed for about half an hour at about 14 knots in bow seas before the failure of the visor attachments. The significant wave height has been estimated by different meteorological institutes to 4.0 - 4.1 m at 0100 hrs at the accident site. Based on the results from model tests and numerical simulations, the Commission has evaluated a probable range of maximum wave loads on the visor during this last period.
The long model test series in bow seas with a significant wave height of 4.5 m is used as the prime basis for the evaluation. Weibull probability distributions have been fitted to the different load components measured at the test. As shown by the long numerical simulations, this type of distribution seems to be valid even down to very low levels of probability. From the basic distributions, extreme value distributions for 30 minutes of exposure time have been calculated, and from these the most probable maximum loads and the range of maximum loads for a 90 % confidence interval. The analysed model test is summarised in Table 12.4. Since the number of recorded load peaks per 30 minutes was low, the range of evaluated probable maximum values becomes wide. Especially the X and Y moments, which have a significantly lower shape parameter, k, than the forces, show a large spread in the distribution of maximum values. The Z moment distribution was not analysed in detail.

Table 12.4 Summary of wave load probability distributions for the model test: Hs = 4.5 m, 150° bow sea, 14.5 knots speed.

Load type	Cumulative probability distribution			Maximum value during 30 min.
[MN] [MNm]	Weibull: F(x) = 1-exp(-(x/b)k) parameters:		No. of load peaks per 30 min	Exceed. probab- ility 0.95	Most pro- bable max.	Exceed. probab- ility 0.05
	b	k	n
X force	1.41	1.04	50	3.85	5.23	9.01
Y force	0.58	0.93	11	0.85	1.49	3.53
Z force	1.40	1.05	53	3.86	5.20	8.86
X moment	1.00	0.60	8	1.28	3.39	14.88
Y moment	5.11	0.81	11	7.97	15.04	40.71

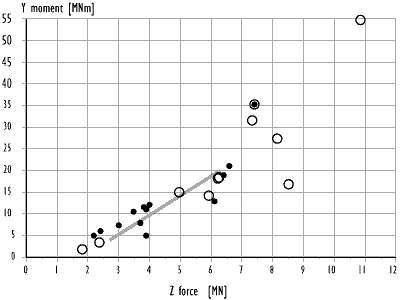
Finally, the loads for the accident condition were roughly estimated by reducing the model test loads with respect to the differences in significant wave height, 4.5 m and 4.0 - 4.1 m respectively. The forces were reduced by 30 % and the moments by 50 %. The level of reduction in forces is taken from the numerical simulations, see Table 12.3 and Figure 12.9, while the reduction in moments is based on an analysis of the correlation between forces and moments, Figure 12.10.

Figure 12.10 Correlation between vertical forces and opening moments from model tests. Rings show the single highest measured value in the different series, black dots show the 13 highest values in the test with bow sea and Hs=4.5 m. The line shows the estimated range of maximum loads for the accident condition.

The Commission's estimate of maximum wave loads on the bow visor for the accident conditions is summarised in Table 12.5. Since the waves in the model tests had rather high crests compared to their troughs, this estimate may be on the high side. On the other hand, the uncertainty in sea state is, according to the meteorological institutes, about 0.5 m in significant wave height. Were this uncertainty also accounted for, the maximum values in the given range would increase significantly.

Table 12.5 Summary of estimated maximum wave loads for the accident conditions. Oblique bow sea, Hs 4.0–4.1 m.

Load type	Load direction	Maximum value during 30 min.
		Range of 90% confidence	Most probable
Visor forces:
X force (longitudinal)	aft	2.7 - 6.3 MN	3.6 MN
Y force (side)	starboard	0.6 - 2.5 MN	1.0 MN
Z force (vertical)	upward	2.7 - 6.2 MN	3.6 MN
Deck hinge moments:
X moment	upward on port side	0.6 - 7.4 MNm	1.7 MNm
Y moment	opening around hinges	4.0 - 20.0 MNm	7.5 MNm
Z moment	fwd. on port side	0.5 - 2.5 MNm	1.0 MNm

To analyse the general situation on board the ESTONIA with regard to wave-induced motions, numerical predictions have been made by applying the linear strip theory and the linear superposition principle. The strip theory underlies a very well known numerical method which has been validated in many comparisons with model and full-scale experimental results. In the present case also the theoretical results show good correlation with experiments.
Main attention has been paid to passenger comfort as dictated by vertical accelerations, to green water on deck and to bottom slamming. The full report on wave-induced motions is included in the Supplement.
The numerical predictions were made for long-crested irregular seas defined by JONSWAP and ISSC wave spectra. The wave periods corresponding to the spectrum peaks, the modal periods, were 7.0, 7.8, 8.5 and 9.5 s. In the case of 7.8 s, which is close to the wave period at the time of the accident, wave-induced motions were also computed in short-crested seas. The significant wave height used was always 4 m, i.e. the estimate of the conditions prevailing at the time of the accident.
The effect of ship speed on the wave-induced motions was examined assuming speeds of 7, 12, 15 and 17 knots. The headings to waves were 180° i.e. head seas, and 150° and 120° representing bow oblique seas. The Estonia encountered the waves slightly on her port bow.

12.4.2 Results

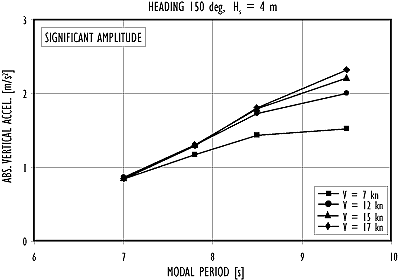
The numerical results show in general that modal wave period and heading to waves have a greater effect on wave-induced motions than does forward speed within the wave periods and headings considered here. Significant motion amplitudes increase with increasing wave period and when the heading to waves changes from direct head seas towards beam seas. The motions were larger in short-crested seas than in long-crested with the exception of the heading 120°. The results indicate that the waves during the accident night were relatively short compared to the length of the ship and she was more or less running through the waves, in particular before midnight.
Just before the accident the significant amplitude of vertical acceleration at the bow visor was 2 - 2.5 m/s2 and the largest amplitudes may have been about 0.4g. This acceleration level is roughly half of the level at which cargo vessels change heading or slow down to decrease the accelerations, and about two thirds of the corresponding level for ro-ro cargo vessels.
In the fore part of the passenger compartment shortly before the accident, the vertical accelerations significantly exceeded the severe discomfort boundary of the Motion Sickness Standard ISO 2631/3. The corresponding ISO boundary value is 1.0 m/s2 in terms of a significant amplitude corresponding to a motion sickness incidence (vomiting) of 10 %. About 20 % of the passengers in the ESTONIA's fore cabins may have been seasick. Amidships the vertical accelerations were significantly below the ISO boundary value and aft they were approximately at that value. Before midnight, when the wave height was smaller, the vertical accelerations were at least 25 % less than just before the accident.
A reduction in speed from 15 knots to 7 knots would have decreased the significant vertical acceleration from about 1.5 m/s2 to 1.3 m/s2 in the fore part of the passenger compartment, or at the station of the bridge (Figure 12.11). By changing the heading to waves, the acceleration level would have started significantly decreasing in stern-quartering waves. Considerably higher vertical accelerations than these predicted for the ESTONIA have been measured on board passenger vessels in severe storms in many sea areas including the Baltic.

Figure 12.11 Vertical acceleration at the station of the bridge in bow sea with Hs=4 m.

The water level at the bow rose above the level of the car deck at nearly every wave encounter due to the combined vertical motion of bow and wave surface. On average, one wave in a hundred, i.e. one every five minutes, reached the level of the upper edge of the ramp opening. From here, there was still 2.5 m freeboard to the stemhead. On these occasions, spray and water reached the foredeck. Survivors have stated generally that there was quite a lot of spray and water flying in the air with occasional submergence of the bow. However, serious amounts of green water on the foredeck were rare as were real bottom slams. Flare impacts probably occurred much more frequently than bottom slams.

It has been discovered both from the sonar investigations of fragments on the seabed and from manoeuvring simulations that the ESTONIA made a port turn at an early stage of the accident. To determine whether the port turn could possibly have been initiated spontaneously by the ship's changed hydrodynamic characteristics when she started to heel in forward speed, a series of model tests was carried out at SSPA Maritime Dynamics Laboratory in conjunction with the wave load tests. A full report of the test results is given in the Supplement.
The self-propelled model of the ESTONIA was run in calm water and in bow seas respectively at a forward speed of 14.5 knots. During running, different weights were placed on the ship side, causing static heel angles from 9o to 27o. With the autopilot working there were no problems to maintain a straight course using only moderate rudder angles. With the rudders locked, the ship had a tendency to turn in the same direction as the heel angle i.e. a starboard list would cause a starboard turn. There were no significant differences in behaviour when the weights were placed at different longitudinal positions.
From the model tests it can be concluded that the possible port turn at an early stage of the capsize was not initiated by the changed hydrodynamic characteristics of the ship in heeled condition. However, the tests were carried out without any wind. From manoeuvring simulations, it has been shown that with locked rudders and decreasing speed a bow wind would cause the ship to turn towards the wind, but not fully through the wind over to the other side.

Theoretical studies were ordered by the Commission to clarify and simulate the rapid flooding, capsize and sinking of the ESTONIA. These studies include analysis of hydrostatic floating conditions and stability, wave-induced motions in heeled condition and water inflow rate on the car deck in the initial phase of the capsize. The full reports are included in the Supplement. Below is given only a brief summary of the major results.

12.6.1 Floating conditions and stability during flooding

New stability calculations were carried out for the Commission, based on the latest valid inclination test. The calculations confirm that for the loading condition of the accident voyage the ESTONIA satisfied the two-compartment damage stability requirements specified in the SOLAS 1974 Convention. The damage stability requirements concern only the watertight part of the vessel below the bulkhead deck, i.e. below the car deck in this case.
The initial stability of a ro-ro ferry with a large open car deck is extremely sensitive to water ingress to the car deck. Small amounts of water will impair upright stability and cause extensive heel in equilibrium condition.
The ESTONIA's static stability with various amounts of water on the car deck has also been analysed. Figure 12.12 shows static stability curves for increasing amounts of water on the car deck, from 0 to 4,000 t. These curves apply when ship side is intact. The analysis shows that 400 t of water on the car deck will give a static list angle of just over 10° and 1,000 t just over 20° (Figure 12.13). The additional heel from a sharp turn at 15 knots would be about 3°.

Figure 12.12 ESTONIA’s static stability curves for different amounts of water on the car deck, ship side assumed intact.

Figure 12.13 ESTONIA’s list against the amount of water on the car deck.

Even though the list developed rapidly, the water on the car deck would not alone be sufficient to make the ship capsize and lose its survivability. As long as the hull was intact and watertight below and above the car deck, the residual stability with water on the car deck would not have been significantly changed at large heel angles (Figure 12.12). The capsize could only have been completed through water entering other areas of the vessel.
According to the hydrostatic calculations, a continuously increasing amount of water on the car deck would make the aft windows of deck 4 the first possible flooding point to other areas (Figure 12.14). Soon thereafter the windows and the aft entrance doors of deck 5 would also be submerged. A little less than 2,000 t of water on the car deck would be sufficient to bring the first flooding points down to the mean water surface. In this condition the list would be about 35°. The lowest corner of the ramp opening would here be still a little above the mean water surface.

Figure 12.14 Freeboard to first possible flooding points plotted against amount of water on car deck. The openings are aft side windows on decks 4 and 5 at frame #6, bow ramp starboard corner, aft door on deck 5 and fore door on deck 5.

As soon as water was free to enter the accommodation decks all residual stability would be impaired and the ship in practice lost. Without an intact superstructure above deck 4, the largest possible equilibrium heel angle before a complete capsize would be 40°. This condition would be exceeded with about 2,000 t of water on the car deck.
Stability calculations show that the ESTONIA would have had a small positive initial stability if the two sauna compartments and the next compartment aft on deck 0 had been flooded. The stability would have been worst at the initial phases of flooding and would have improved when more water flowed to these three compartments.
The influence of cargo shifting was also investigated in separate studies. Due to the distribution of vehicles on deck, the maximum transverse shifting of cargo centre of gravity could have been of the order of just a few metres. Two metres of cargo shift would have the effect that the progressive flooding of deck 4 started with about 10 % less water on the car deck.

12.6.2 Water inflow simulations

The water inflow through the ramp opening after the visor had failed and was lost was simulated with two different numerical methods. One is similar to the numerical wave impact load simulation, i.e. an approach where the relative motions between bow and waves are described in the time domain. The other approach uses the frequency distribution of relative motions.
The common input to the simulations is:

• A description of relative motion in a random sea condition,
• a description of the relative velocity of water particles in the ship's longitudinal direction as a function of vertical position, wave profile and the ship's heading and speed,
• a description of the changing floating condition during water ingress.

Results obtained from the simulations are very sensitive to small changes in the initial parameters, and the inherent uncertainty in the random nature of waves and ship motions during short periods of time is very large. Therefore, the results cannot be used to independently prove a certain time sequence of water inflow. The value of the simulations is primarily to verify whether the assumed capsizing scenario is possible with regard to the water inflow rate.
During the first phase of the accident, the ESTONIA is assumed to have been sailing at a speed of about 14 knots into bow-incoming waves with a significant wave height of about 4 m. The average water inflow at the instant when the ramp was torn fully open has been calculated to be in the range of 300 - 600 t/min depending on what assumption is made regarding forward freeboard in running condition (Figures 12.15 and 12.16). This means that within just one or a few minutes a heel angle of about 20° could possibly have developed.

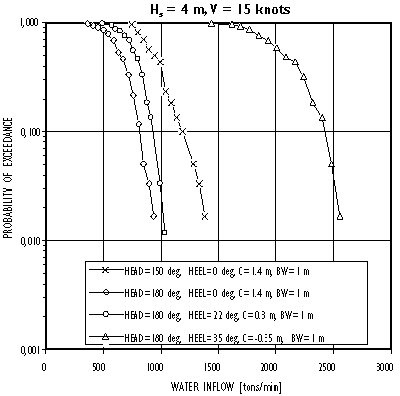
Figure 12.15 Probability of exceedance for different amounts of water inflow to car deck through bow ramp opening in bow and head seas at 15 knots speed with list angle as a parameter. C = Freeboard to the starboard corner of ramp, BW = bow wave height.

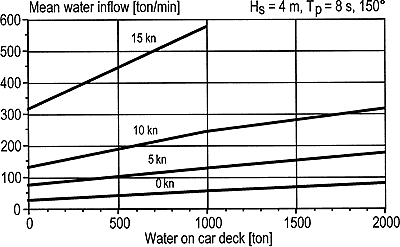
Figure 12.16 Mean water inflow as function of ship speed and amount of water on car deck in bow sea.

The successive phases of the capsize are dealt with in more detail further on in this report, where the time sequence and the full capsize scenario are analysed based on witnesses' statements and an interpretation of the results obtained from these simulations. Here the general influence of changing conditions is briefly summarised.
The speed of the vessel greatly influences the inflow rate. If the speed is reduced from 15 to 10 knots, the inflow rate in head and bow seas decreases by about 50 %. This effect is due partly to reduced inflow velocity and partly to reduced bow wave height.
The amount of water on the car deck also affects the inflow rate. When the ship heels over, the freeboard to the ramp opening decreases and the inflow accelerates. To some extent this effect is contradicted by changed motion characteristics in heeled condition. The separate studies produced some differences regarding the motion characteristics and the results diverged with respect to heel angles; however, the inflow rate is generally 2 - 3 times larger than the initial upright condition when 1,800 t has entered the car deck and the heel is around 35°.
Wave direction also affects water inflow. The highest rate of inflow is found in bow sea due to large relative motion amplitudes. In beam sea the inflow rate is very low as long as the speed and heel angle are not excessive.
The simulations indicate that the time from the first inflow through the ramp opening until progressive flooding of accommodation deck 4 started was about of 5 - 15 min. However the time estimates depend greatly on what action is assumed to have been taken during the first critical minutes.

Continues...